贝叶斯算法实现拼写纠错和垃圾邮件分类 Implementation of Bayesian Algorithm for Spell Correction and Spam Classification

背景 Background

贝叶斯公式能解决哪类问题呢？下面就以一个日常生活中经常遇到的问题为例。我们打字的时候是不是经常出现拼写错误，但是程序依旧会返回正确拼写的字或者语句。这时候程序就会猜测：‘这个用户真正想输入的单词是什么呢？

What kind of problems can the Bayesian formula solve? Let's take an example from everyday life. When we type, isn't it common to make spelling errors? However, the program still returns the correctly spelled word or phrase. At this point, the program will guess: 'What word is the user actually trying to input?

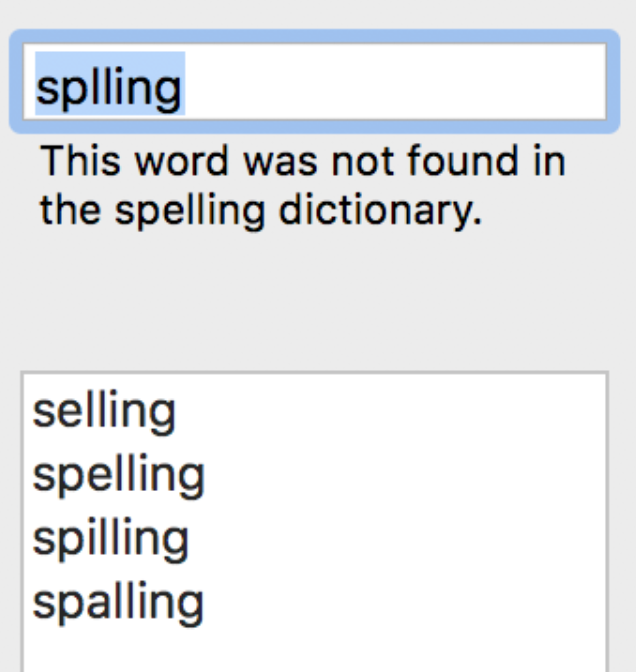
原理 Principle

贝叶斯公式的原理是A和B同时发生的概率相同

The principle of the Bayesian formula is that the probability of A and B happening simultaneously is the same.

先验概率：在得到新信息之前，对某个事件发生的主观或客观的初始估计。它是基于已有的知识或历史数据的一个初始判断。

后验概率：在观察到新证据或数据之后，对某个事件发生概率的更新估计。它结合了先验概率和新的数据，反映了在新信息下重新评估事件发生的可能性。

Prior Probability: An initial subjective or objective estimate of the likelihood of an event occurring before any new information is obtained. It is a preliminary judgment based on existing knowledge or historical data.

Posterior Probability: An updated estimate of the likelihood of an event occurring after observing new evidence or data. It combines the prior probability with the new data and reflects a reassessment of the event's likelihood in light of the new information.

纠错分析 Analysis of Spell Correction

例如，用户本来想输入‘the’，但是由于打字错误，输成‘tha’，那么程序能否猜出他到底想输入哪个单词呢？可以用下式表示：

P(猜测他想输入的单词 | 他实际输入的单词)

"For example, if a user intended to type 'the' but mistakenly typed 'tha' due to a typing error, can the program guess which word they actually meant to input? This can be expressed by the formula: 

P(guessing the word they meant to input | the word they actually typed).

例如，用户实际输入的单词记为D（D代表一个具体的输入，即观测数据），那么可以有很多种猜测：猜测1，P(h1|D)；猜测2，P(h2|D)；猜测3，P(h3|D)等。例如h1可能是the，h2可能是than，h3可能是then，到底是哪一个呢？也就是要比较它们各自的概率值大小，哪个可能性最高就是哪个。先把上面的猜想统一为P(h|D)，然后进行分析。直接求解这个公式好像难度有些大，有点无从下手，但是刚刚不是得到贝叶斯公式吗？转换一下能否好解一些呢？先来试试看：

For instance, let's denote the word the user actually typed as D (D represents a specific input, i.e., observed data). There can be various guesses: guess 1, P(h1|D); guess 2, P(h2|D); guess 3, P(h3|D), and so on. For example, h1 might be 'the', h2 might be 'than', and h3 might be 'then'. Which one is it? It comes down to comparing the probability values for each and choosing the one with the highest likelihood. First, let's generalize the above guesses to P(h|D), and then analyze it. Directly solving this equation seems a bit difficult, and it's hard to know where to start. But didn't we just derive the Bayesian formula? Maybe by transforming it, we can make it easier to solve. Let's give it a try:

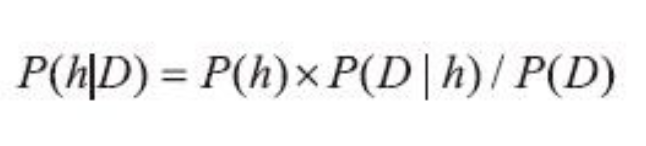
此时该如何理解这个公式呢?实际计算中，需要分别得出分子和分母的具体数值，才能比较最终结 果的大小，对于不同的猜测h1、h2、h3......，分母D的概率P(D)相同，因为都是相同的输入数据，由于只 是比较最终结果的大小，而不是具体的值，所以这里可以不考虑分母，也就是最终的结果只和分子成正 比的关系，化简可得:

How should we understand this formula at this point? In actual calculations, we need to separately determine the specific values of the numerator and denominator to compare the final result's magnitude. For different guesses h1, h2, h3, etc., the denominator, P(D), is the same because the input data is the same. Since we are only comparing the magnitude of the final results, not their specific values, we can ignore the denominator. Thus, the final result is only proportional to the numerator, and we can simplify it as follows:

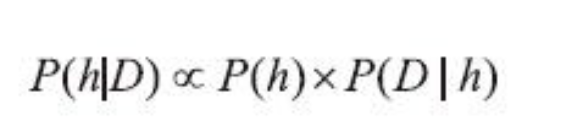
对于给定观测数据，一个猜测出现可能性的高低取决于以下两部分。

• P(h):表示先验概率，它的大小可以认为是事先已经计算好了的，比如有一个非常大的语料库，里 面都是各种文章、新闻等，可以基于海量的文本进行词频统计。

• P(D|h):表示这个猜测生成观测数据的可能性大小，一般使用编辑距离计算，听起来有点抽象，还是举一个例子。例如猜想 的这个词h需要通过几次增删改查能得到观测结果D，这里可以认为通过一次操作的概率值要高于两次， 毕竟你写错一个字母的可能性高一些，一次写错两个就是不可能的。

For a given observed data, the likelihood of a guess depends on the following two components:

• P(h): This represents the prior probability, which can be considered pre-calculated. For example, if there is a very large corpus containing various articles, news, etc., word frequency statistics can be gathered based on the massive amount of text.

• P(D|h): This represents the likelihood of this guess producing the observed data, generally calculated using edit distance. This might sound a bit abstract, so let's look at an example. Suppose the guessed word h requires a certain number of insertions, deletions, or substitutions to arrive at the observed result D. It's reasonable to assume that the probability of a single operation is higher than that of two operations, as the likelihood of making one typo is higher, while making two typos at once is less likely."

后把它们组合在一起，就是最终的结果。例如，用户输入“tlp”(观测数据D)，那他到底输入的 是“top”(猜想h1)还是“tip”(猜想h2)呢?也就是:已知h1=top，h2=tip，D=tlp，求P(top|tlp)和P(tip|tlp)到 底哪个概率大。经过贝叶斯公式展开可得:

Then, by combining them together, we get the final result. For example, if the user inputs 'tlp' (observed data D), did they actually mean to input 'top' (guess h1) or 'tip' (guess h2)? That is: given h1=top, h2=tip, and D=tlp, we need to determine whether P(top|tlp) or P(tip|tlp) has the higher probability. By expanding the Bayesian formula, we obtain:

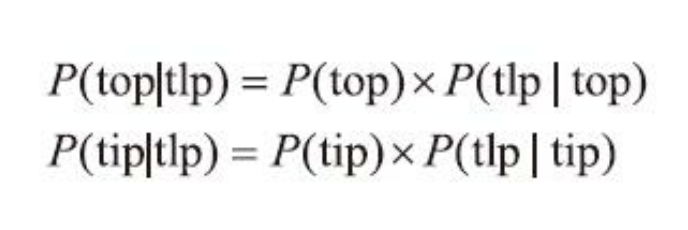
这个时候，看起来都是写错了一个词，假设这种情况下，它们生成观测数据的可能性相同， 即P(tlp|top)=P(tlp|tip)，那么最终结果完全由P(tip)和P(top)决定，也就是之前讨论的先验概率。一般情况下，如果语料库文本数据中top出现的可能性更高，那么其先验概率更大，最终的结果就是h1:top

At this point, it seems that both words have a single letter error. If we assume that the likelihood of them producing the observed data is the same, i.e., P(tlp|top) = P(tlp|tip), then the final result is entirely determined by P(tip) and P(top), which corresponds to the prior probability we discussed earlier. Generally, if the word 'top' is more likely to appear in the corpus text data, then its prior probability is higher, leading to the final result being h1:top.

代码实现 Implementation of Code

import re
from collections import Counter

# 读取文本并创建词频字典
# Read text and create a frequency dictionary of words
def words(text):
    return re.findall(r'\w+', text.lower())

# 这里用一个简单的文本作为词库
# Use a simple text as the word corpus
WORDS = Counter(words("""
apple apply application banana orange apply top tip top
"""))

# 计算词的概率
# Calculate the probability of a word
def P(word, N=sum(WORDS.values())):
    return WORDS[word] / N

# 生成编辑距离为1的单词
# Generate words that are one edit distance away from the input word
def edits1(word):
    letters    = 'abcdefghijklmnopqrstuvwxyz'
    splits     = [(word[:i], word[i:]) for i in range(len(word) + 1)]
    deletes    = [L + R[1:] for L, R in splits if R]
    transposes = [L + R[1] + R[0] + R[2:] for L, R in splits if len(R) > 1]
    replaces   = [L + c + R[1:] for L, R in splits if R for c in letters]
    inserts    = [L + c + R for L, R in splits for c in letters]
    return set(deletes + transposes + replaces + inserts)

# 生成编辑距离为2的单词
# Generate words that are two edit distances away from the input word
def edits2(word):
    return (e2 for e1 in edits1(word) for e2 in edits1(e1))

# 返回已知单词
# Return known words from a list of words
def known(words):
    return set(w for w in words if w in WORDS)

# 拼写校正
# Spell correction function
def correct(word):
    candidates = known([word]) or known(edits1(word)) or known(edits2(word)) or [word]
    return max(candidates, key=P)

# 示例
# Example usage
print(correct("tlp"))

垃圾邮件分类 Spam Classification

接下来再看一个日常生活中的实例——垃圾邮件分类问题。这里涉及到另一个关键词——朴素贝叶斯，在原有的问题上加上一层独立的假设，就是朴素贝叶斯，其实理解起来还是很简单的，它 强调了特征之间的相互独立

Next, let's look at an example from everyday life— the spam classification problem. This involves another key concept—Naive Bayes. By adding an assumption of independence to the original problem, we get Naive Bayes. In fact, it's quite simple to understand, as it emphasizes the independence between features.

本例中用D表示收到的这封邮件，注意D并不是一个大邮件，而是由N个单词组成的一个整体。 用h+表示垃圾邮件，h−表示正常邮件。当收到一封邮件后，只需分别计算它是垃圾邮件和正常邮件可能 性是多少即可，也就是P(h+|D)和P(h−|D)。

In this example, we use D to represent the received email. Note that D is not one large email but a whole made up of N words. Let h+ represent a spam email and h− represent a normal email. When an email is received, you just need to calculate how likely it is to be spam or a normal email, that is,  P(h+∣D) and P(h−∣D).

import re
from collections import defaultdict


# Helper function to tokenize and clean text
def tokenize(text):
    text = text.lower()
    return re.findall(r'\b\w+\b', text)


# Training data: some example spam and normal emails
spam_emails = [
    "Win money now",
    "Cheap loans available",
    "Click here to claim your prize",
    "You have won a lottery"
]

normal_emails = [
    "Meeting schedule",
    "Let's have lunch tomorrow",
    "Project deadline is next week",
    "Can we reschedule the call?"
]

# Step 1: Calculate the prior probabilities P(spam) and P(normal)
num_spam = len(spam_emails)
num_normal = len(normal_emails)
total_emails = num_spam + num_normal

P_spam = num_spam / total_emails
P_normal = num_normal / total_emails

# Step 2: Tokenize the emails and calculate the word frequencies for spam and normal emails
spam_word_counts = defaultdict(int)
normal_word_counts = defaultdict(int)

# Count word frequencies in spam emails
for email in spam_emails:
    words = tokenize(email)
    for word in words:
        spam_word_counts[word] += 1

# Count word frequencies in normal emails
for email in normal_emails:
    words = tokenize(email)
    for word in words:
        normal_word_counts[word] += 1

# Total number of words in spam and normal emails
total_spam_words = sum(spam_word_counts.values())
total_normal_words = sum(normal_word_counts.values())


# Step 3: Define a function to compute P(word | spam) and P(word | normal)
def word_prob(word, word_counts, total_words, alpha=1):
    # Use Laplace smoothing to handle unseen words
    return (word_counts[word] + alpha) / (total_words + alpha * 2)


# Step 4: Define the Naive Bayes classification function
def classify(email):
    words = tokenize(email)

    # Calculate the log probabilities to avoid underflow
    log_spam_prob = 0
    log_normal_prob = 0

    for word in words:
        # Calculate P(word | spam) and P(word | normal) with Laplace smoothing
        log_spam_prob += word_prob(word, spam_word_counts, total_spam_words)
        log_normal_prob += word_prob(word, normal_word_counts, total_normal_words)

    # Multiply by the prior probabilities P(spam) and P(normal)
    spam_score = P_spam * log_spam_prob
    normal_score = P_normal * log_normal_prob

    # Return the classification based on which score is higher
    if spam_score > normal_score:
        return "Spam"
    else:
        return "Not Spam"


# Step 5: Test the classifier with new emails
test_emails = [
    "Win a prize now",
    "Schedule a meeting",
    "Click here to win money",
    "Let's have lunch"
]

# Classify each test email
for email in test_emails:
    print(f"Email: '{email}' -> {classify(email)}")