博客内容Blog Content
推荐系统原理 Principle of Recommender Systems
本节介绍推荐系统的原理,包括用户和商品的协同过滤算法和以及隐含矩阵的计算 This section introduces the principles of recommender systems, including collaborative filtering algorithms for users and items, as well as the computation of latent matrices.
背景 Background
大数据与人工智能时代,互联网产品发展迅速,竞争也越来越激烈,而推荐系统在其中发挥了决定 性的作用。例如,某人观看抖音的时候,特别喜欢看篮球和游戏的短视频,只要打开APP,就都是熟悉的 旋律,系统会推荐各种精彩的篮球和游戏集锦,根本不用自己动手搜索。广告与新闻等产品也是如此, 都会抓住用户的喜好,对症下药才能将收益最大化,这都归功于推荐系统,本章向大家介绍推荐系统中 的常用算法。
In the era of big data and artificial intelligence, internet products are developing rapidly, and competition is becoming increasingly fierce. Recommender systems play a decisive role in this context. For example, when someone watches Douyin and particularly enjoys short videos about basketball and games, as soon as they open the app, they are greeted with familiar content. The system recommends various exciting basketball and game highlights, eliminating the need to search manually. The same applies to products like advertisements and news, which capture users' preferences and tailor content to maximize profits. This is all thanks to recommender systems. This chapter introduces commonly used algorithms in recommender systems.
协同过滤算法 Collaborative Filtering Algorithm
如果大家想邀请朋友去看一场电影,你的首选对象是谁?应该是自己的好朋友吧,因为你们有共同 的爱好。现在有几部电影同时上映,实在拿不定主意选哪一部,该怎么办呢?这时可能会有两种方案。
1. 问问各自的好朋友,因为彼此的品位差不多,朋友喜欢的电影,大概也符合你的口位。
2.回忆一下看过的喜欢的电影,看看正在上映的这些电影中,哪部与之前看过的类似。 问题是如何让计算机确定哪个朋友跟你的喜好相同呢?如何确定哪一部新的电影与你之前看过的类似呢?这些任务可以通过协同过滤来完成,也就是通过用户和商品的画像数据进行相似度计算
If you want to invite a friend to watch a movie, who would you choose first? It would probably be your close friend, because you share similar interests. Now, if there are several movies showing at the same time and you can't decide which one to pick, what would you do? At this point, there might be two options:
1. Ask your close friends, because you have similar tastes; if your friend likes the movie, it's likely that it will suit your preferences as well.
2. Think back to movies you've enjoyed in the past and see if any of the currently showing movies are similar to those.
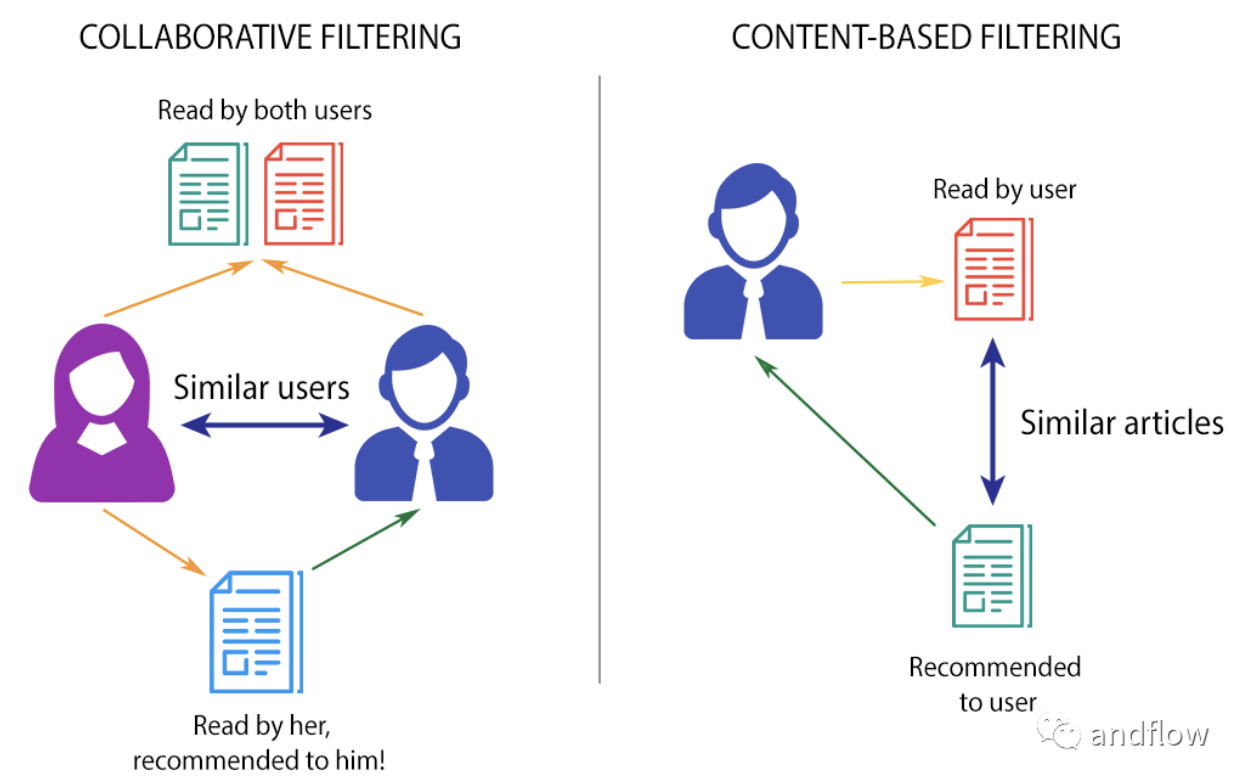
基于用户的协同过滤:找最相似的朋友,看看他们喜欢什么,推荐与当前用户行为相似的其他用户喜欢的物品。
基于物品的协同过滤:找看过的商品,看看哪些比较类似,推荐与用户曾经喜欢的物品相似的其他物品。
User-based Collaborative Filtering: Find the most similar friends, see what they like, and recommend items that other users with similar behaviors to the current user have liked.
Item-based Collaborative Filtering: Look at the products you've experienced and see which ones are similar, then recommend items that are similar to those the user has previously liked.
基于用户的协同过滤 User-based Collaborative Filtering
首先来看一下基于用户的协同过滤,假设有5组用户数据,还有用户对两种商品的评分,通过不同的评分,计算哪些用户的品位比较相似。
Let's first take a look at user-based collaborative filtering. Suppose we have data from five groups of users and their ratings for two products. By comparing these different ratings, we can calculate which users have similar tastes.
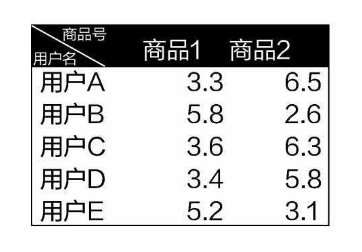
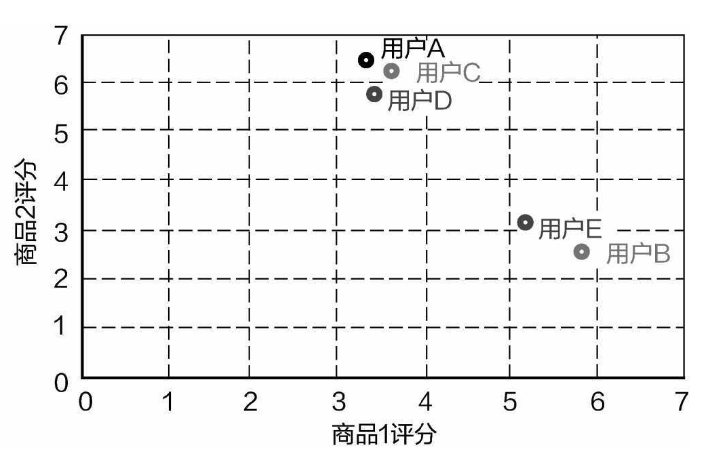
最直接的方法是,把用户和评分数据展示在二维平面上,如图13-6所示。很明显,用户A、C、D应该是一类人,他们对商品1都不太满意,而对商品2比较满意。用户E和B是另外一类,他们的喜好与用户A、C、D正好相反。
The most straightforward method is to display the users and their rating data on a two-dimensional plane, as shown in Figure 13-6. It's clear that users A, C, and D belong to one group, as they are not very satisfied with Product 1 but are more satisfied with Product 2. Users E and B form another group, with preferences opposite to those of A, C, and D.
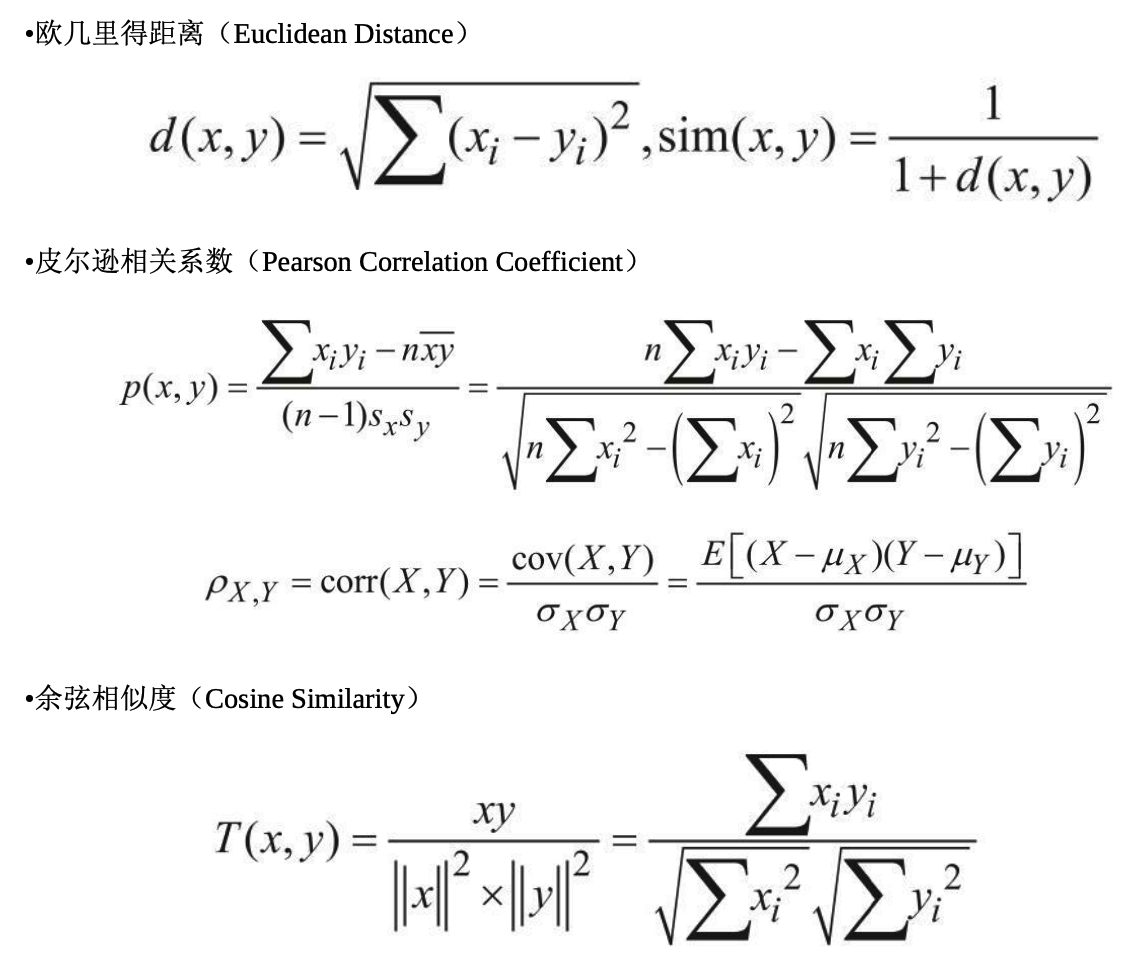
只要有数据,计算相似度的方法比较多,下面列出几种常见的相似度计算方法:
There are many methods to calculate similarity as long as data is available. Below are some common similarity calculation methods:
在基于用户的推荐中,一旦通过相似度计算找到那些最相近的用户,就可以看看他们的喜好是什 么,如果在已经购买的商品中,还有一件商品是待推荐用户还没有购买的,把这件商品推荐给用户即 可。
In user-based recommendations, once the most similar users have been identified through similarity calculations, we can then look at their preferences. If there is a product that these similar users have already purchased but the user to whom we're making the recommendation has not yet bought, we can recommend that product to the user.
基于物品的协同过滤 Item-based Collaborative Filtering
基于商品的协同过滤在原理上和基于用户的基本一致,只不过变成要计算商品之间的相似度。
Item-based collaborative filtering is fundamentally similar to user-based collaborative filtering, except that it focuses on calculating the similarity between items.
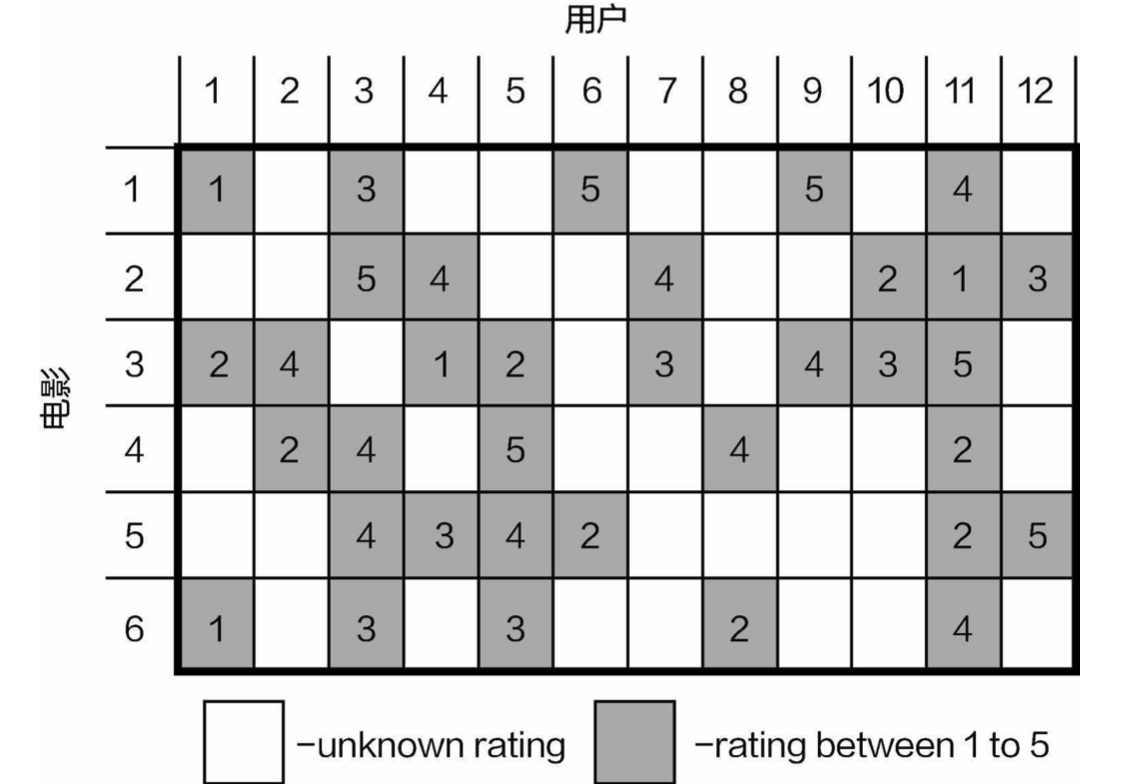
来看一个实际的例子,如图所示,有12个用户,6部电影,可以把它们当作一个矩阵,其中的 数值表示用户对电影的评分。空着的地方表示用户还没有看过这些电影,其实做推荐就是要估算出这些 空值都可能是什么,如果某一处得到较高的值,意味着用户很可能对这个电影感兴趣,那就给他推荐这 个电影。
Let’s consider a practical example. As shown in Figure, there are 12 users and 6 movies, which can be represented as a matrix. The numbers in the matrix indicate the users' ratings of the movies. The blank spaces represent movies that the users have not yet watched. In fact, making recommendations involves estimating what these blank values might be. If a particular blank space receives a high estimated value, it means the user is likely to be interested in that movie, and the system can then recommend it to them.
此时任务已经下达,要对5号用户进行推荐,也就是要分别计算该用户对所有未看过电影的可能评 分,以其中一部电影的计算方法为例,其他位置的计算方法相同。例如想求5号用户对1号电影的喜好程 度,假设已经通过某种相似度计算方法得到1号电影和其他电影的相似度(例如通过比对电影类型、主 演、上映时间等信息),由于5号用户之前看过3号电影和6号电影(相似度为负分的暂时不考虑),所以 需要分别考虑这两部电影和1号电影的相似度,计算方法如图
At this point, the task has been set: we need to make recommendations for User 5 by calculating the potential ratings for all the movies they haven’t seen yet. Let’s take one movie as an example to illustrate the process, with the same method applied to other movies. Suppose we want to determine how much User 5 would like Movie 1. Assume we have already calculated the similarity between Movie 1 and other movies (e.g., by comparing features such as genre, lead actors, release date, etc.). Since User 5 has previously watched Movie 3 and Movie 6 (we temporarily ignore movies with negative similarity scores), we need to consider the similarities between these two movies and Movie 1. The calculation method is shown in the diagram.
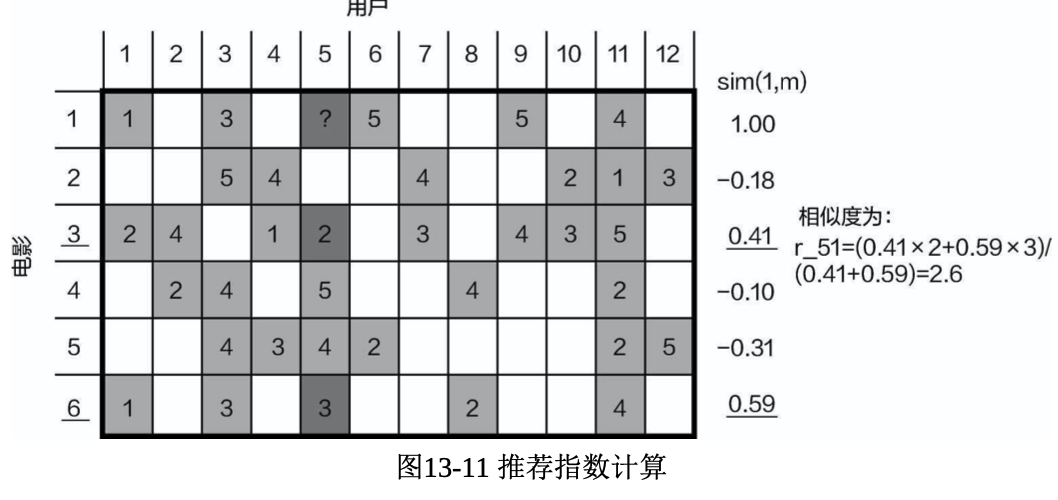
这里可以把相似度看作权重项,相似度越高,起到的作用越大,最后再进行归一化处理即可。最终 求得5号用户对1号电影的评分值为2.6,看来他可能不喜欢1号电影。
Here, we can treat the similarity as a weighting factor: the higher the similarity, the greater its impact on the final score. Afterward, we normalize the result. The final calculated rating for User 5’s preference for Movie 1 is 2.6, suggesting that they probably won’t like Movie 1 very much.
隐含矩阵 Latent Matrices
协同过滤方法虽然简单,但是其最大的问题就是计算的复杂度,如果用户-商品矩阵十分庞大,这个计算量可能是难以忍受的
Although collaborative filtering is simple, its biggest drawback is the computational complexity. If the user-item matrix is enormous, the amount of computation can become unbearable.
稀疏矩阵的问题在于考虑的是每一个用户和每一个商品之间的联系,那么,能否换一种思路呢?假设有10万个用户和10万个商品,先不考虑它们之间直接的联系,而是引进“中介”,每个“中介”可以服务1000个商品和1000个用户,那么,只需要100个“中介”就可以完成任务。此时就将原始的用户-商品问题转换成用户-中介和中介-商品问题,也就是把原本的一个庞大的矩阵转换成两个小矩阵。
The problem with sparse matrices is that they consider the relationships between every user and every item. So, is there a different approach we could try? Suppose we have 100,000 users and 100,000 items. Instead of directly considering the relationships between them, we introduce "intermediaries." Each intermediary could handle 1,000 items and 1,000 users. In this case, only 100 intermediaries would be needed to complete the task. This transforms the original user-item problem into a user-intermediary and intermediary-item problem, effectively splitting one large matrix into two smaller matrices.
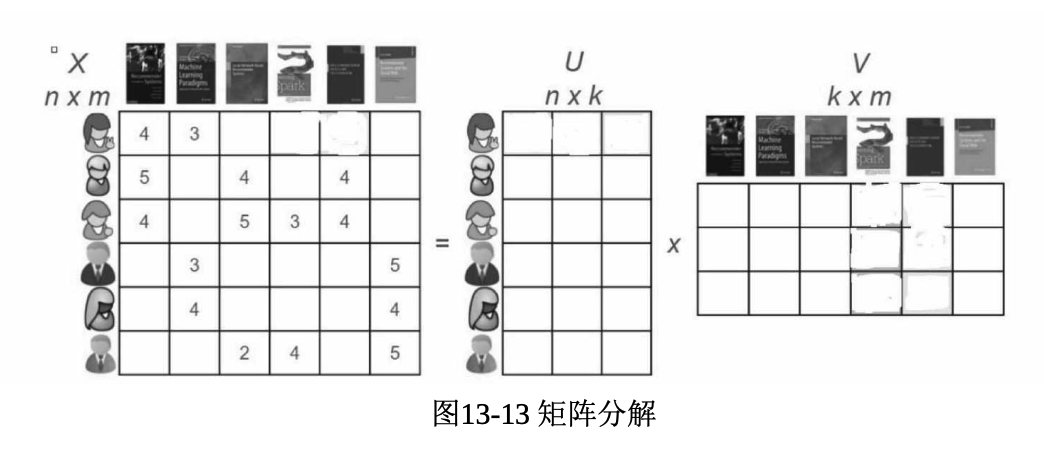
矩阵分解的目的就是希望其规模能够缩减,更方便计算,现阶段推荐系统基本都是基于矩阵分解实现的
The goal of matrix factorization is to reduce the scale of the problem, making it easier to compute. Currently, most recommender systems are implemented based on matrix factorization.
隐含矩阵的计算 computation of latent matrices
如何求解隐语义模型呢?其实在推荐系统中,想得到的结果就是稀疏矩阵中那些为0的值可能是什 么,也就是想看一下用户没有买哪些商品。首先计算出其购买各种商品的可能性大小,然后依照规则选 出最有潜力的商品即可。其中的难点在于如何构建合适的隐含因子来帮助化简矩阵,如图所示,F是要求解的隐含因 子,只需要把它和用户与商品各自的联系弄清楚即可。
How do we solve for the latent semantic model? In fact, in a recommender system, the goal is to estimate the values of the zeros in a sparse matrix, which means predicting the items that a user has not yet purchased. The first step is to calculate the likelihood that a user will purchase various items, and then select the most promising items based on predefined rules. The challenge lies in how to construct appropriate latent factors to help simplify the matrix, as shown in the diagram. The latent factor F is what we need to solve for, and we only need to clarify its connections with both users and items.

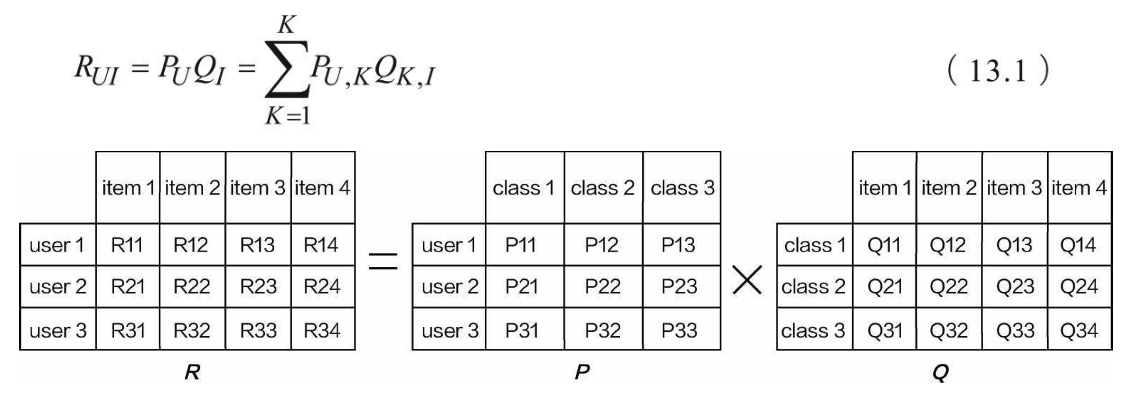
R矩阵可以分解成P矩阵和Q矩阵的乘积,如图所示。此时只需分别求解出P和Q,自然就可以还 原回R矩阵:
The matrix R can be decomposed into the product of matrix P and matrix Q, as shown in the figure. At this point, once we solve for P and Q, we can naturally reconstruct the original matrix R:
按照机器学习的思想,可以把隐含因子当作要求解的参数,依旧还是这个老问题,什么样的参数能 够更符合实际的数据,先指定一个目标函数:
In line with the principles of machine learning, we can treat the latent factors as parameters to be solved. This brings us back to the familiar problem: what parameters best fit the actual data? First, we specify an objective function:
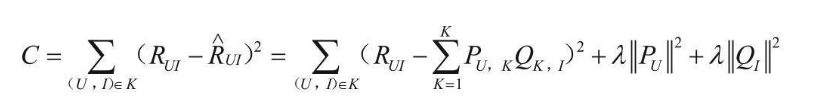
看起来与回归中的最小二乘法有点类似,计算由隐含因子还原回来的矩阵与原始矩阵的差异程度, 并且加入正则化惩罚项。
The objective function resembles the least squares method in regression, where we compute the difference between the matrix reconstructed from the latent factors and the original matrix, and we add a regularization penalty term.
按照之前回归中的求解思路,此时可以利用梯度下降进行迭代优化,首先计算梯度方向:
Following the solution approach used in regression, we can use gradient descent for iterative optimization. First, we calculate the gradient direction:
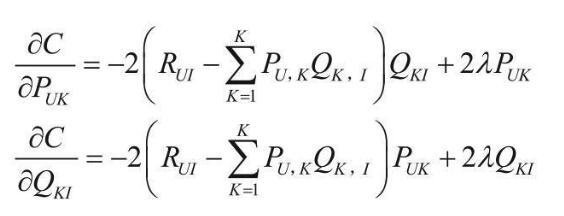
接下来按照给定方向,选择合适的学习率进行更新即可:
Next, we update in the given direction by selecting an appropriate learning rate to adjust the parameters accordingly: