博客内容Blog Content
Java&FlinkML实现在线线性回归 OnlineLinear Regression Implementation in Java and FlinkML
Java和FlinkML线性回归的梯度下降实现,并自己实现一个支持在线学习的模型 Implementation of gradient descent in Java and FlinkML linear regression, along with a self-implemented model that supports online learning.
概述 Introduction
线性回归是统计学和机器学习中一种常见的方法。求解线性回归问题的方法有很多
Linear regression is a common method in both statistics and machine learning. There are many ways to solve linear regression problems.
最小二乘法(Ordinary Least Squares, OLS)
最常见的线性回归求解方法是最小二乘法,其目标是最小化预测值与实际值的平方误差和
The most common method for solving linear regression is the Ordinary Least Squares (OLS), whose goal is to minimize the sum of squared errors between the predicted values and the actual values.
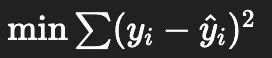
通过矩阵运算计算回归系数
The regression coefficients can be computed through matrix operations.
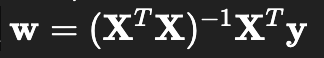
梯度下降法(Gradient Descent)
当数据量很大时,直接求解 OLS 可能计算代价较高。此时可以使用梯度下降法,通过迭代更新回归系数,逐步逼近最优解
When the dataset is large, directly solving OLS can be computationally expensive. In this case, the gradient descent method can be used, where the regression coefficients are iteratively updated to gradually approach the optimal solution.
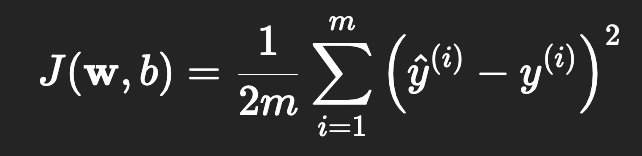
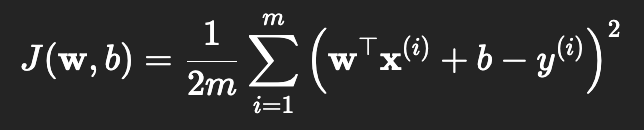
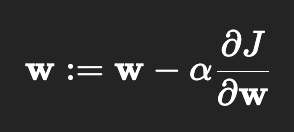
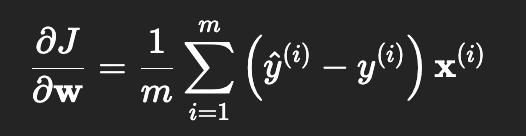
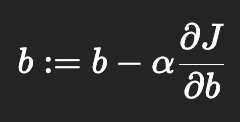
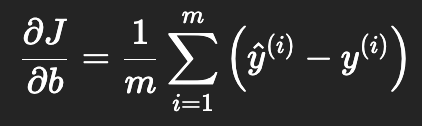
随机梯度下降法(Stochastic Gradient Descent, SGD)
随机梯度下降法是梯度下降的一种变体,它每次只使用一个或少量样本进行参数更新,适合处理大规模数据。
Stochastic Gradient Descent (SGD) is a variant of gradient descent. It updates the parameters using only one or a small subset of samples at a time, making it suitable for handling large-scale data.
JAVA中的实现
The implementation in JAVA
以下为一个梯度下降的JAVA实现
Below is a Java implementation of gradient descent:
package flink.example;
public class GradientDescent {
// 定义学习率和迭代次数
// Define learning rate and number of iterations
private static final double LEARNING_RATE = 0.01;
private static final int ITERATIONS = 10000;
public static void main(String[] args) {
// 示例数据集:两个输入特征 x1 和 x2,输出 y
// Example dataset: two input features x1 and x2, output y
double[][] x = {
{1, 2}, // x1 = 1, x2 = 2
{2, 4}, // x1 = 2, x2 = 4
{3, 6}, // x1 = 3, x2 = 6
{4, 8}, // x1 = 4, x2 = 8
{5, 10} // x1 = 5, x2 = 10
};
double[] y = {5, 10, 15, 20, 25};
// 初始化回归系数
// Initialize regression coefficients
double w1 = 0;
double w2 = 0;
double w0 = 0;
// 梯度下降算法
// Gradient descent algorithm
for (int i = 0; i < ITERATIONS; i++) {
// 计算各方向的梯度
// Compute gradients in each direction
double[] gradients = computeGradients(x, y, w1, w2, w0);
// 更新参数 w1, w2 和 w0
// Update parameters w1, w2, and w0
w1 -= LEARNING_RATE * gradients[0];
w2 -= LEARNING_RATE * gradients[1];
w0 -= LEARNING_RATE * gradients[2];
// 输出当前迭代的信息
// Output information of the current iteration
if (i % 100 == 0) {
System.out.printf("Iteration %d: w1 = %.4f, w2 = %.4f, w0 = %.4f, Cost = %.4f%n",
i, w1, w2, w0, computeCost(x, y, w1, w2, w0));
}
}
// 输出最终结果
// Output the final result
System.out.printf("Final result: w1 = %.4f, w2 = %.4f, w0 = %.4f%n", w1, w2, w0);
}
// 求解梯度,相当于是求解各方向的变化率,具体实现是用的是损失函数(平方差)的求导
// Compute gradients, essentially the rate of change in each direction.
// This is done via the derivative of the loss function (squared error)
private static double[] computeGradients(double[][] x, double[] y, double w1, double w2, double w0) {
double gradientW1 = 0;
double gradientW2 = 0;
double gradientW0 = 0;
int n = x.length;
// 用全量样本计算
// Compute with all samples
for (int i = 0; i < n; i++) {
double prediction = w1 * x[i][0] + w2 * x[i][1] + w0;
double error = prediction - y[i];
// 计算各方向的梯度
// Compute gradients in each direction
gradientW1 += error * x[i][0];
gradientW2 += error * x[i][1];
gradientW0 += error;
}
return new double[]{(gradientW1 / n), (gradientW2 / n), (gradientW0 / n)};
}
// 计算损失函数 (均方误差)
// Compute the cost function (Mean Squared Error)
private static double computeCost(double[][] x, double[] y, double w1, double w2, double w0) {
double totalError = 0;
int n = x.length;
for (int i = 0; i < n; i++) {
double prediction = w1 * x[i][0] + w2 * x[i][1] + w0;
totalError += Math.pow(prediction - y[i], 2);
}
return totalError / (2 * n);
}
}如果使用随机梯度下降,代码只需做对应修改
If using stochastic gradient descent, the code only needs the corresponding modifications.
// 随机梯度下降算法
// Stochastic Gradient Descent algorithm
for (int epoch = 0; epoch < EPOCHS; epoch++) {
// 随机选一个样本
// Randomly select a sample
int i = random.nextInt(n); // 使用 Random 生成随机索引 Generate a random index using Random
// 计算预测值
// Compute prediction
double prediction = w1 * x[i][0] + w2 * x[i][1] + w0;
// 计算误差
// Compute error
double error = prediction - y[i];
// 计算梯度
// Compute gradients
double gradientW1 = error * x[i][0];
double gradientW2 = error * x[i][1];
double gradientW0 = error;
// 更新参数
// Update parameters
w1 -= LEARNING_RATE * gradientW1;
w2 -= LEARNING_RATE * gradientW2;
w0 -= LEARNING_RATE * gradientW0;
// 每隔一定轮数输出一次当前状态
// Output current status every certain number of epochs
if ((epoch + 1) % 1000 == 0) { // 每 1000 个 epoch 输出一次结果 Output every 1000 epochs
double cost = computeCost(x, y, w1, w2, w0);
System.out.printf("Epoch %d: w1 = %.4f, w2 = %.4f, w0 = %.4f, Cost = %.4f%n",
epoch + 1, w1, w2, w0, cost);
}
}FlinkML中的实现
The implementation in FlinkML
FlinkML也有对应线性回归的实现,值得注意的是这里似乎不支持在线学习(流式计算),只能离线训练出模型再预测数据
FlinkML also has an implementation for linear regression. It is worth noting that it does not seem to support online learning (stream processing); you can only train the model offline and then use it for prediction.
另外,需要注意需要根据数据的范围和特点,调整对应的学习率的迭代次数才能得到比较准确的结果
Additionally, it is important to adjust the learning rate and the number of iterations according to the range and characteristics of the data to obtain more accurate results.
以下为一个FlinkML线性回归的例子
Below is an example of FlinkML linear regression.
package flink.regression;
import org.apache.flink.ml.linalg.DenseVector;
import org.apache.flink.ml.linalg.Vectors;
import org.apache.flink.ml.regression.linearregression.LinearRegression;
import org.apache.flink.ml.regression.linearregression.LinearRegressionModel;
import org.apache.flink.streaming.api.datastream.DataStream;
import org.apache.flink.streaming.api.environment.StreamExecutionEnvironment;
import org.apache.flink.table.api.Table;
import org.apache.flink.table.api.bridge.java.StreamTableEnvironment;
import org.apache.flink.types.Row;
import java.util.*;
public class LinearRegressionExample {
public static void main(String[] args) throws Exception {
StreamExecutionEnvironment env = StreamExecutionEnvironment.getExecutionEnvironment().setParallelism(1);
StreamTableEnvironment tEnv = StreamTableEnvironment.create(env);
// 生成训练和测试数据,label = f(x, y),数据范围会影响对应需要的学习率和迭代次数
// Generate training and testing data: label = f(x, y), the data range will affect the required learning rate and number of iterations
List<Row> trainData = new ArrayList<>();
for (double x = 1; x <= 100; x++) {
for (int y = 1; y <= 100; y++) {
trainData.add(Row.of(Vectors.dense(x, y), f(x, y), 1.0));
}
}
List<Row> testData = new ArrayList<>();
for (double x = 130; x <= 150; x++) {
for (int y = 120; y <= 150; y++) {
testData.add(Row.of(Vectors.dense(x, y), f(x, y), 1.0));
}
}
// 数据流转换为表
// Convert data streams to tables
DataStream<Row> trainStream = env.fromCollection(trainData);
Table trainTable = tEnv.fromDataStream(trainStream).as("features", "label", "weight");
DataStream<Row> testStream = env.fromCollection(testData);
Table testTable = tEnv.fromDataStream(testStream).as("features", "label", "weight");
// 使用LR(梯度下降实现)训练数据得到模型,较小的学习率要对应较大的迭代次数
// 这个模型不支持Online在线流式学习,只能提前算好模型再预测
// Train a model using LR (implemented with gradient descent), where a smaller learning rate requires more iterations
// This model doesn't support online streaming learning, it only works by precomputing the model and then making predictions
LinearRegression lr = new LinearRegression()
.setFeaturesCol("features")
.setLabelCol("label")
.setWeightCol("weight")
.setLearningRate(0.0001)
.setMaxIter(1000000);
LinearRegressionModel lrModel = lr.fit(trainTable);
// 使用模型进行预测
// Make predictions using the trained model
Table outputTable = lrModel.transform(testTable)[0];
// 提取并显示结果
// Extract and display results
DataStream<String> predictionStream = tEnv.toDataStream(outputTable)
.map(row -> {
DenseVector features = (DenseVector) row.getField(lr.getFeaturesCol());
double expectedResult = (Double) row.getField(lr.getLabelCol());
double predictionResult = (Double) row.getField(lr.getPredictionCol());
return String.format(
" Features: %s, Expected: %f => Predicted: %f",
features,
expectedResult,
predictionResult
);
});
predictionStream.printToErr();
// 显示模型参数
// Display model parameters
DataStream<String> coefficientStream = tEnv.toDataStream(lrModel.getModelData()[0])
.map(row -> {
DenseVector coefficient = (DenseVector) row.getField("coefficient");
return String.format("Coefficient: %s", coefficient);
});
coefficientStream.printToErr();
// 执行作业
// Execute the job
env.execute("LinearRegressionExample");
}
private static double f(double x, double y) {
return 3 * x + 2 * y;
}
}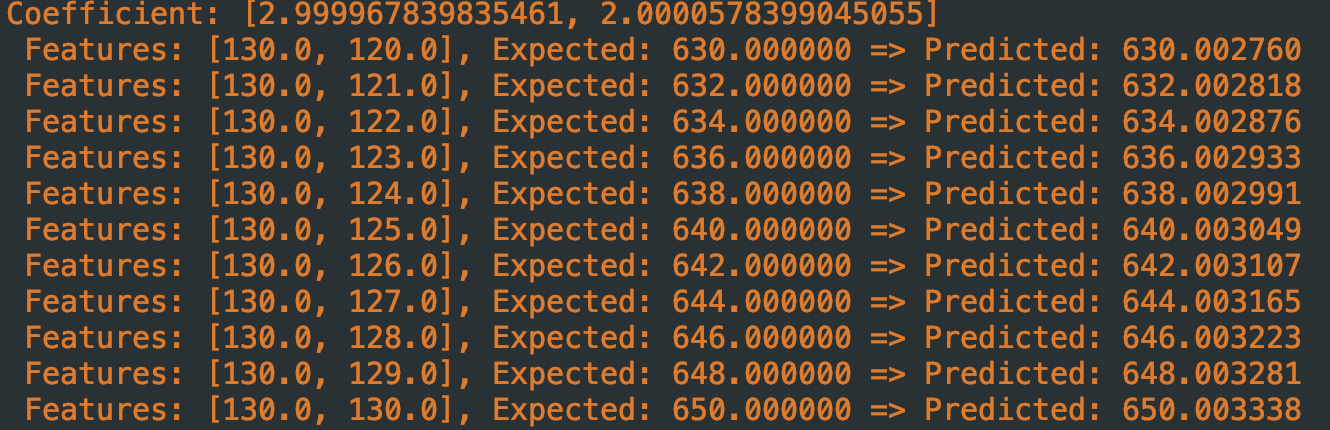
目前看计算效果还是不错的,但如果参数(学习率、迭代次数)不合适,结果会很离谱
Currently, the computation results are quite good, but if the parameters (learning rate, number of iterations) are not appropriate, the results can be very inaccurate.
实现一个在线的线性回归模型
Implement an online linear regression model
FlinkML不支持在线的线性回归,我们自己可以手动实现一个在线版线性回归(基于随机梯度下降实现)以支持实时流式计算
FlinkML does not support online linear regression, but we can manually implement an online version of linear regression (based on stochastic gradient descent) to support real-time stream processing.
package flink.regression;
import org.apache.flink.api.common.state.ValueState;
import org.apache.flink.api.common.state.ValueStateDescriptor;
import org.apache.flink.api.common.typeinfo.Types;
import org.apache.flink.api.java.tuple.Tuple2;
import org.apache.flink.ml.linalg.DenseVector;
import org.apache.flink.streaming.api.datastream.DataStream;
import org.apache.flink.streaming.api.environment.StreamExecutionEnvironment;
import org.apache.flink.streaming.api.functions.co.CoProcessFunction;
import org.apache.flink.streaming.api.functions.source.SourceFunction;
import org.apache.flink.util.Collector;
import java.util.Arrays;
public class OnlineLinearRegressionStream {
public static void main(String[] args) throws Exception {
StreamExecutionEnvironment env = StreamExecutionEnvironment.getExecutionEnvironment().setParallelism(1);
// 生成训练数据
// Generate training data
DataStream<Tuple2<DenseVector, Double>> trainStream = env.addSource(new TrainDataSource());
// 生成测试数据
// Generate testing data
DataStream<Tuple2<DenseVector, Double>> testStream = env.addSource(new TestDataSource());
// 连接训练流和测试流
// Connect the training stream and testing stream
DataStream<String> predictionStream = trainStream.connect(testStream)
.keyBy(tuple -> 0, tuple -> 0)
// 统一分区处理
// Partition the data uniformly
.process(new OnlineLinearRegressionFunction(0.0001))
.name("OnlineLinearRegression");
predictionStream.printToErr();
env.execute("OnlineLinearRegressionExample");
}
// 简单的线性函数作为标签
// Simple linear function as label
private static double f(double x, double y) {
return 3 * x + 2 * y;
}
// 自定义的在线线性回归函数
// Custom online linear regression function
public static class OnlineLinearRegressionFunction extends CoProcessFunction<Tuple2<DenseVector, Double>, Tuple2<DenseVector, Double>, String> {
private final double learningRate;
private ValueState<DenseVector> weightsState;
public OnlineLinearRegressionFunction(double learningRate) {
this.learningRate = learningRate;
}
@Override
public void open(org.apache.flink.configuration.Configuration parameters) {
ValueStateDescriptor<DenseVector> descriptor =
new ValueStateDescriptor<>("weights", Types.GENERIC(DenseVector.class));
weightsState = getRuntimeContext().getState(descriptor);
}
@Override
public void processElement1(Tuple2<DenseVector, Double> value, Context ctx, Collector<String> out) throws Exception {
// 训练数据流
// Training data stream
DenseVector weights = weightsState.value();
if (weights == null) {
// 初始化权重
// Initialize weights
weights = new DenseVector(new double[]{0.0, 0.0});
}
double prediction = dot(weights, value.f0);
double error = value.f1 - prediction;
// 简单的SGD更新
// Simple SGD update
double[] newWeights = new double[weights.size()];
for (int i = 0; i < weights.size(); i++) {
newWeights[i] = weights.values[i] + learningRate * error * value.f0.values[i];
}
System.out.println(value + " -> " + Arrays.toString(newWeights));
weights = new DenseVector(newWeights);
weightsState.update(weights);
}
@Override
public void processElement2(Tuple2<DenseVector, Double> value, Context ctx, Collector<String> out) throws Exception {
// 测试数据流
// Testing data stream
DenseVector weights = weightsState.value();
if (weights == null) {
weights = new DenseVector(new double[]{0.0, 0.0});
}
double prediction = dot(weights, value.f0);
String result = String.format("Features: %s, Expected: %f => Predicted: %f",
value.f0, value.f1, prediction);
out.collect(result);
}
private double dot(DenseVector a, DenseVector b) {
double sum = 0.0;
for (int i = 0; i < a.size(); i++) {
sum += a.values[i] * b.values[i];
}
return sum;
}
}
static class TrainDataSource implements SourceFunction<Tuple2<DenseVector, Double>> {
private volatile boolean isRunning = true;
@Override
public void run(SourceContext<Tuple2<DenseVector, Double>> ctx) throws Exception {
for (double x = 1; x <= 100; x++) {
for (int y = 1; y <= 100; y++) {
double label = f(x, y);
ctx.collect(new Tuple2<>(new DenseVector(new double[]{x, y}), label));
Thread.sleep(10);
if (!isRunning) break;
}
}
}
@Override
public void cancel() {
isRunning = false;
}
}
static class TestDataSource implements SourceFunction<Tuple2<DenseVector, Double>> {
private volatile boolean isRunning = true;
@Override
public void run(SourceContext<Tuple2<DenseVector, Double>> ctx) throws Exception {
for (double x = 130; x <= 150; x++) {
for (int y = 120; y <= 150; y++) {
double label = f(x, y);
ctx.collect(new Tuple2<>(new DenseVector(new double[]{x, y}), label));
Thread.sleep(100);
if (!isRunning) break;
}
}
}
@Override
public void cancel() {
isRunning = false;
}
}
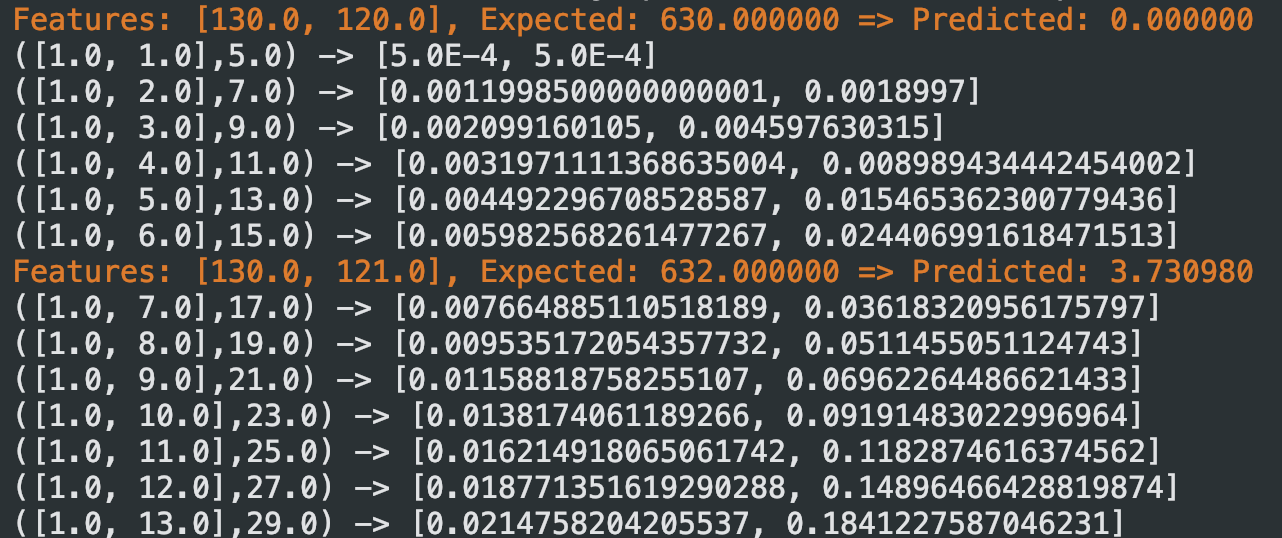
}可以看到刚运行时,偏差较大,但参数也在逐步更新
At the beginning of the run, we can see that the bias is quite large, but the parameters are gradually being updated.
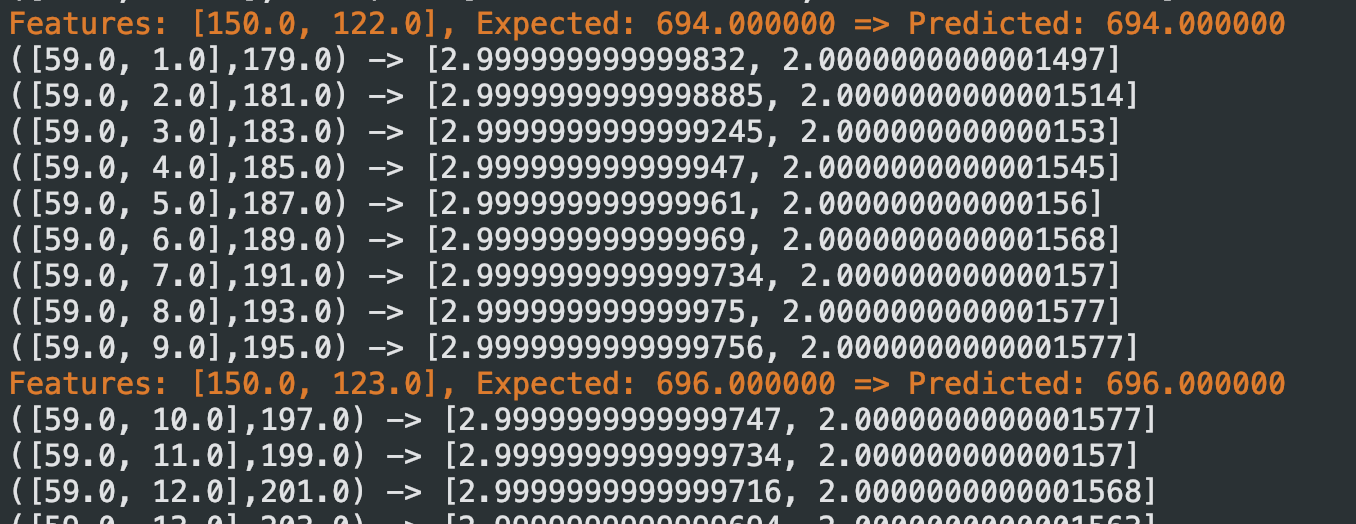
运行一段时间后,调整后的参数逐渐接近真实参数,预测值也越来越准,接近标签值
After running for a while, the adjusted parameters gradually approach the true parameters, and the predictions become more accurate, approaching the label values.
在线学习的挑战 Challenges of Online Learning
尽管在线学习有其优势,但在实践中,批处理方法仍然在很多场景中占据主导地位,而在线学习方法(如随机梯度下降,SGD)可以用于线性回归和 KMeans,但它们在实现时需要克服一些困难:
噪声问题:在在线学习中,每次使用一个或少量数据进行更新,可能会导致模型对噪声非常敏感。相比之下,批处理方法可以通过平均化多个样本来减少噪声的影响。
模型收敛速度:在线学习依赖于每次小步更新,因此通常需要较多的迭代才能收敛,而批处理方法每次更新考虑所有数据,可能在更少的迭代中就能达到较好的结果。
参数更新的稳定性:在线学习中的每次参数更新都可能导致模型剧烈变化,特别是在高维数据或稀疏数据的情况下。通过批处理方法,模型在每次更新中考虑了全局信息,参数更新相对更加稳定。
Although online learning has its advantages, in practice, batch processing still dominates in many scenarios. While online learning methods (such as Stochastic Gradient Descent, SGD) can be used for linear regression and KMeans, they come with certain challenges during implementation:
Noise issue: In online learning, updating the model using one or a small amount of data at a time can make the model very sensitive to noise. In contrast, batch processing methods can reduce the impact of noise by averaging multiple samples.
Model convergence speed: Online learning depends on small updates with each step, so it usually requires more iterations to converge. Batch processing methods, on the other hand, consider all the data in each update, potentially reaching better results in fewer iterations.
Stability of parameter updates: Each parameter update in online learning can lead to drastic changes in the model, especially in the case of high-dimensional or sparse data. Batch processing methods, by considering global information in each update, allow for more stable parameter updates.
