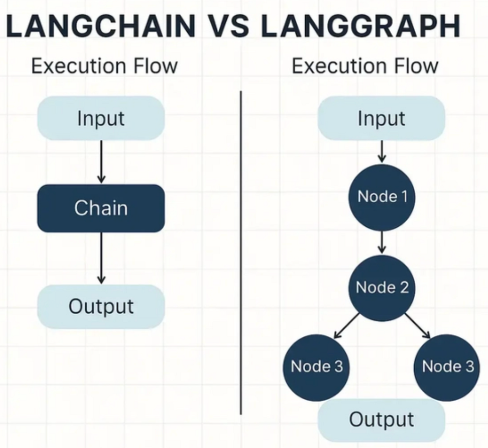
利用LangGraph优化新闻汇总 Optimize news summarization using a LangGraph workflow
利用LangGraph对爬取的新闻数据进行节点任务编排,更灵活地操作和生成数据 Use LangGraph to orchestrate node-based tasks on scraped news data, enabling more flexible data manipulation and generation